Giáo dục, tham khảo > Đề thi - Đáp án

Đề thi vào lớp 10 môn Toán trường THPT chuyên Hùng Vương, Phú Thọ năm 2013

Cho biểu thức: 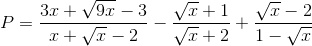P=frac{3x+sqrt{9x}-3}{x+sqrt{x}-2}-frac{sqrt{x}+1}{sqrt{x}+2}+frac{sqrt{x}-2}{1-sqrt{x}}  với x ≥ 0, x ≠ 1.

 

Câu 1:Rút gọn biểu thức P.

Câu 2:Tìm x nguyên dương để P nhận giá trị nguyên.

Câu 3:Cho hệ phương trình 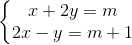left{egin{matrix} x+2y=m\ 2x-y=m+1 end{matrix} ight.

Tìm m để hệ phương trình có nghiệm (x; y) sao cho x, y là độ dài các cạnh góc vuông của một góc vuông có độ dài cạnh huyền bằng sqrt{5}

Câu 4:Tìm các số tự nhiên x, y thỏa mãn phương trình: x2 + 2y2 + 2xy + 3y – 4  = 0

Câu 5:Giải phương trình: 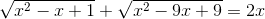sqrt{x^{2}-x+1}+sqrt{x^{2}-9x+9}=2x

Câu 6:Giải hệ phương trình: 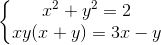left{egin{matrix} x^{2}+y^{2}=2\ xy(x+y)=3x-y end{matrix} ight.

 

Cho hai đường tròn (O) và (O') cắt nhau tại A, B . Kẻ tiếp tuyến chung CD (C, D là tiếp điểm và C thuộc (O), D thuộc (O')). Qua B kẻ cát tuyến song song với CD cắt (O) tại E cắt (O') tại F. Gọi M, N theo thứ tự là giao điểm của DA và CA với EF. Gọi I là giao điểm của EC với FD. Chứng minh rằng:

 

Câu 7:CD là trung trực của đoạn BI.

Câu 8:Tam giác MIN cân.

Câu 9:Cho A là điểm cố định trên đường tròn (O; R). Gọi AB và AC là hai dây cung thay đổi của đường tròn (O) thỏa mãn 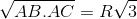sqrt{AB.AC}=Rsqrt{3} . Xác định vị trí của B, C trên (O) để diện tích tam giác ABC lớn nhất.

Câu 10:Cho a, b, c dương thỏa mãn 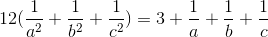12(frac{1}{a^{2}}+frac{1}{b^{2}}+frac{1}{c^{2}})=3+frac{1}{a}+frac{1}{b}+frac{1}{c}

Chứng minh rằng: 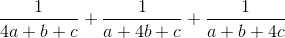frac{1}{4a+b+c}+frac{1}{a+4b+c}+frac{1}{a+b+4c}  ≤ frac{1}{6}

Chưa có câu trả lời nào

CÂU HỎI LIÊN QUAN